Loads Acting on Aircraft

The flight envelope of an aeroplane can be divided into two regimes. The first is rectilinear flight in a straight line, i.e. the aircraft does not accelerate normal to the direction of flight. The second is curvilinear flight, which, as the name suggests, involves flight in a curved path with acceleration normal to tangential flight path. Curvilinear flight is often known as manoeuvring and is of greater importance for structural design since the aerodynamic and inertial loads are much higher than in rectilinear flight.

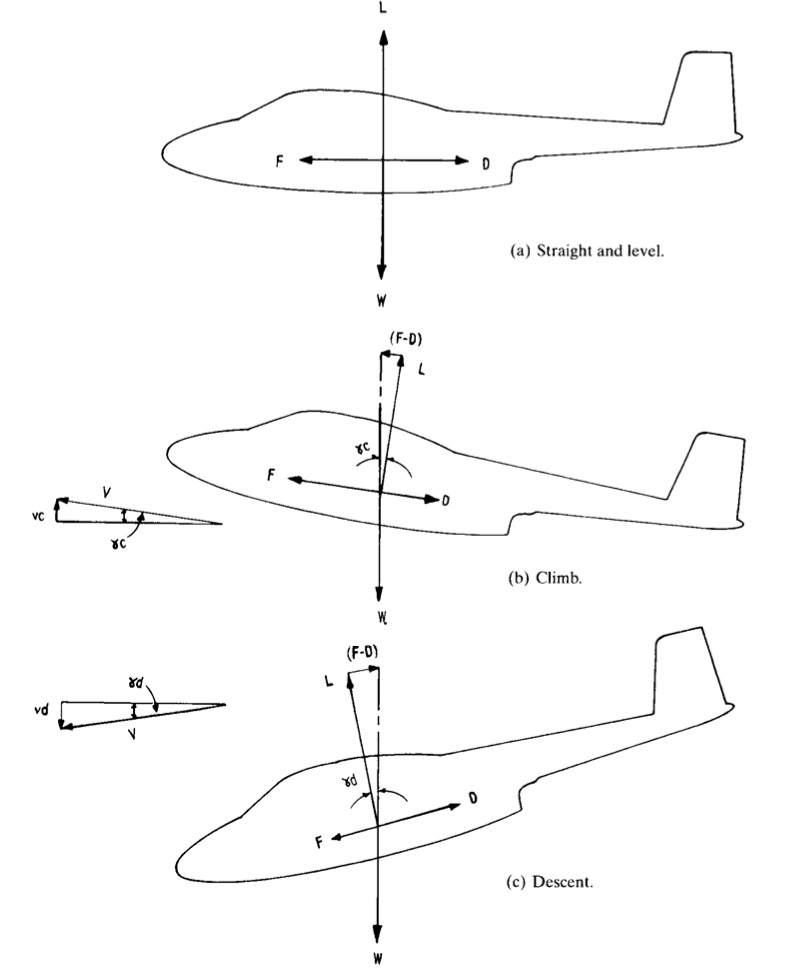
As the aircraft moves relative to the surrounding fluid a pressure field is set up over the entire aircraft, and not only over the wings, that acts to keep the aircraft afloat. This aerodynamic pressure always acts normal to the outer contour of the skin but the resultant force can be resolved into two forces acting tangential and normal to the direction of flight. The sum of the forces normal to the direction of flight give rise to the lift force L, which offsets the weight of the aircraft i.e. offsets the weight of the aircraft W. The tangential components give the resultant drag force D, which in powered flight must be overcome by the propulsive force F. The resultant force F includes the thrust generated by the engines, the induced drag of the propulsive system and the inclination of the line of thrust to the direction of flight. In basic mechanics the aircraft is simplified into a point coincident with the centre of gravity (CG) of the aircraft with all forces assumed to act through the centre of gravity. If the net resultant of a force is offset from the CG then a resultant moment will also act on the aircraft. For example, the lift generated by the wings is generally offset from the centre of gravity of the aircraft and may thus produce a net pitching moment that has to be offset by the control surfaces. Figure 1 below shows as a simplified free body diagram of an aircraft in level flight, climb and descent.

Fig. 1. Free body diagram of aircraft in flight (1)

Note that the lift is only equal and opposite to the weight in steady and level flight, thus:

and

In steady descent and steady climb the lift component is less than the weight, since only a component of the weight acts normal to the direction of flight and because by definition lift is always normal to both drag and thrust. Also in climbing the thrust must be greater than the drag to overcome the component of weight acting against the direction of flight and vice versa in descent. Thus in a climb:

and 

and in descent

, 

This situation is schematically represented in Figure 1 by the relative sizes of the different arrows. In general we can imagine the weight being balanced by the lift force L and the difference between the thrust F and the drag D.  A bit of manipulation of the two equations for climb or descent above gives the same expression,

such that,

The latter expression is clearly obtained if Pythagoras’ rule is applied to the vector triangles that include (F-D) and L in Figure 1.

Figure 1 also shows velocity diagrams depicting the relationship between true air speed V, tangential to the direction of flight, and the rates of climb and descent and respectively. We can combine these velocity triangles with the forces triangles to obtain simple equations for the rates of climb and descent,

and

such that or .

This expression can also be used to gain some insight into the driving factors behind gliding flight. In this case the net propulsive force F is zero such that the expression becomes,

which may be approximated to  since the angle of descent in gliding is typically very shallow. Therefore the gliding efficiency of a sailplane depends on maximising the lift to drag ratio L/D. If the ascending thermals are equal to or greater than this rate of descent than the glider can continuously maintain or even gain in altitude.

An aircraft may of course increase its speed along the direction of rectilinear flight in which case the thrust force F must be greater than the vector sum of the drag and the component of the weight. A more interesting scenario are accelerated flight where the acceleration occurs as a result in change in direction rather than a change in speed. By definition, in vector mechanics a change in direction is a change in velocity and therefore defined as acceleration, even if the magnitude of the speed does not change. A change in the flight path is achieved by changing the magnitude of the overall lift component or by differences in lift between the two wings, away from the equilibrium condition depicted in Figure 1. This change can either be obtained by a change in true airspeed or by changing the angle of attack of the wings relative to the airflow. Consider the simple banked turn in Figure 2 below.

Fig. 2. Free Body Diagram of an aircraft in a banked turn (1)

As the aircraft banks the lift force normal to the wings is turned through an angle from the vertical weight vector. Since the centripetal acceleration acts horizontally and the weight acts vertically we can use simple trigonometric relations to find the radius of turn:

such that . It is also obvious that the more steeply banked the turn the more lift will be required from the wings since,

such that increase in engine power is needed to maintain constant speed under this flight condition. This is one of the reasons why fighter jets that require manoeuvres with very tight radii have such short and stubby wings. Small radii if turn R and thus high banking angles require increases in lift and therefore increase the bending moments acting on the wings.

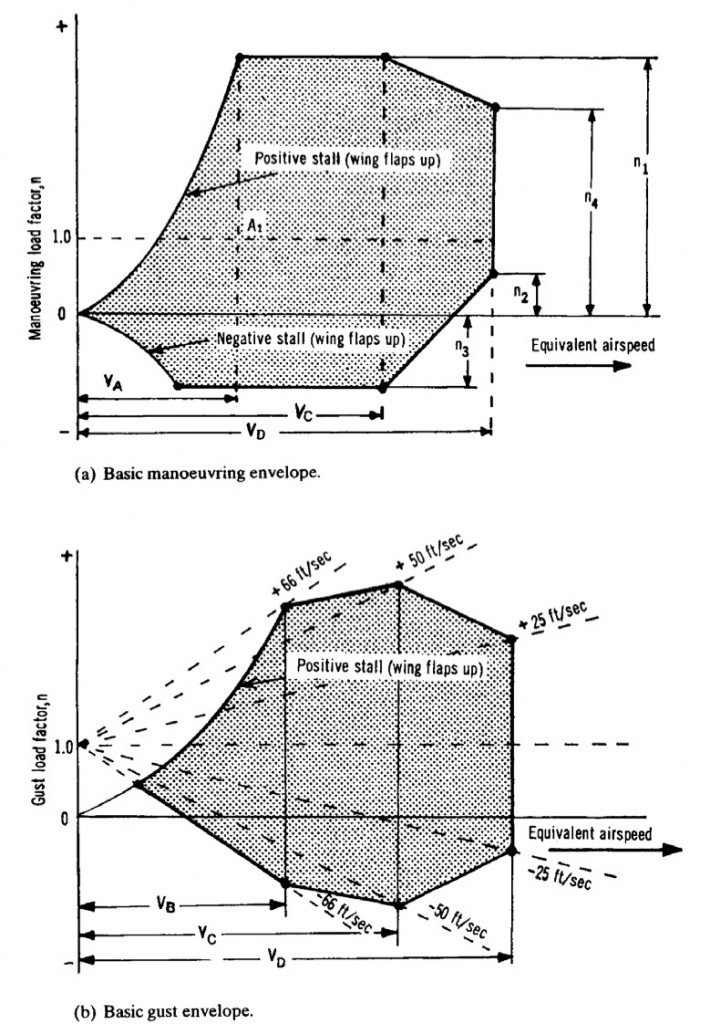
In reality the airplane is subjected to a large variety of different combinations of accelerations (rolls, pull-ups, push-overs, spinning, stalling , gusts etc.) at different velocities and altitudes. In classical mechanics free fall is expressed as having an acceleration 0f -1g and level flight is denoted as 0g. The aeronautical engineer differs from this convention in order to make the comparison between lift and weight simpler. This means that free fall is denoted by 0g and level flight by 1g. The ratio between lift and aircraft weight is called the load factor n, where , i.e. n = 0 for free fall, n = 1 for level flight, n > 1 to pull out of a dive and n < 1 to pull out of a climb. The overall load spectrum of an aircraft is captured graphically by so called velocity – load factor (V-n) curves. The outline of these diagrams are given by the possible combinations of load factor and velocity than an aircraft will be expected to cope with. For example Figure 3a shows the basic V-n diagram for symmetric flight (asymmetric envelopes exist for rolls etc. but are not covered here).

Fig. 2 The a) basic manoeuvre and b) gust flight envelopes (1)

The envelope is constructed from the positive and negative stall lines which indicate, respectively, the maximum and minimum load that can be achieved because of the inability of the aircraft to produce any more lift. Thus,

where is the density of the surrounding air and is the wing surface area. The limiting factor also known as the maximum expected service load is defined by

or 2.5, whichever is greater, with W the max take-off weight.

, and   are defined as the maximum manoeuvre speed ( the speed above which it is unwise to make full application of any single flight control), the design cruise speed and the maximum dive speed, respectively. The intersection between the horizontal line  and the left curve of the envelope is also of special significance since it represents the stall speed at level flight. In general the limit load factor must be tolerable without detrimental permanent deformation. The aircraft must also support an ultimate load (=limit load x safety factor) for at least 3 seconds. The safety factor is generally taken to be 1.5.

Finally, Figure 3b shows a typical gust envelope. A gust alters the angle of attack of the lifting surfaces by an amount equal to where w is the vertical gust velocity. Since the lift scales with the angle of attack up to the point of aerodynamic stall, the inertia forces applied to structure are altered by the gust winds. The gust envelope is constructed with the same stall lines as the basic manoeuvre envelope and different gust lines are drawn radiating from n = 1 at V = 0. Note that the design gust intensities reduce as the velocity increases, with the intention that the aircraft is flown accordingly. In the gust envelope is replaced with , representing the design speed at maximum gust intensity.

References

(1) Stinton, D. The Anatomy of the Airplane. 2nd Edition. Blackwell Science Ltd. (1998).