At the start of the 19th century, after studying the highly cambered thin wings of many different birds, Sir George Cayley designed and built the first modern aerofoil, later used on a hand-launched glider. This biomimetic, highly cambered and thin-walled design remained the predominant aerofoil shape for almost 100 years, mainly due to the fact that the actual mechanisms of lift and drag were not understood scientifically but were explored in an empirical fashion. One of the major problems with these early aerofoil designs was that they experienced a phenomenon now known as boundary layer separation at very low angles of attack. This significantly limited the amount of lift that could be created by the wings and meant that bigger and bigger wings were needed to allow for any progress in terms of aircraft size. Lacking the analytical tools to study this problem, aerodynamicists continued to advocate thin aerofoil sections, as there was plenty of evidence in nature to suggest their efficacy. The problem was considered to be more one of degree, i.e. incrementally iterating the aerofoil shapes found in nature, rather than of type, that is designing an entirely new shape of aerofoil in accord with fundamental physics.
During the pre-WWI era, the misguided notions of designers was compounded by the ever-increasing use of wind-tunnel tests. The wind tunnels used at the time were relatively small and ran at very low flow speeds. This meant that the performance of the aerofoils was being tested under the conditions of laminar flow (smooth flow in layers, no mixing perpendicular to flow direction) rather than the turbulent flow (mixing of flow via small vortices) present over the wing surfaces. Under laminar flow conditions, increasing the thickness of an aerofoil increases the amount of skin-friction drag (as shown in last month’s post), and hence thinner aerofoils were considered to be superior.
The modern plane – born in 1915
The situation in Germany changed dramatically during WWI. In 1915 Hugo Junkers pioneered the first practical all-metal aircraft with a cantilevered wing – essentially the same semi-monocoque wing box design used today. The most popular design up to then was the biplane configuration held together by wires and struts, which introduced considerable amounts of parasitic drag and thereby limited the maximum speed of aircraft. Eliminating these supporting struts and wires meant that the flight loads needed to be carried by other means. Junkers cantilevered a beam from either side of the fuselage, the main spar, at about 25% of the chord of the wing to resist the up and down bending loads produced by lift. Then he fitted a smaller second spar, known as the trailing edge spar, at 75% of the chord to assist the main spar in resisting fore and aft bending induced by the drag on the wing. The two spars were connected by the external wing skin to produce a closed box-section known as the wing box. Finally, a curved piece of metal was fitted to the front of the wing to form the “D”-shaped leading edge, and two pieces of metal were run out to form the trailing edge. This series of three closed sections provided the wing with sufficient torsional rigidity to sustain the twisting loads that arise because the centre of pressure (the point where the lift force can be considered to act) is offset from the shear centre (the point where a vertical load will only cause bending and no twisting). Junker’s ideas were all combined in the world’s first practical all-metal aircraft, the Junker J 1, which although much heavier than other aircraft at the time, developed into the predominant form of construction for the larger and faster aircraft of the coming generation.
Junkers J 1 at Döberitz in 1915
Junkers construction naturally resulted in a much thicker wing due to the room required for internal bracing, and this design provided the impetus for novel aerodynamics research. Junker’s ideas were supported by Ludwig Prandtl who carried out his famous aerodynamics work at the University of Göttingen. As discussed in last month’s post, Prandtl had previously introduced the notion of the boundary layer; namely the existence of a U-shaped velocity profile with a no-flow condition at the surface and an increasing velocity field towards the main stream some distance away from the surface. Prandtl argued that the presence of a boundary layer supported the simplifying assumption that fluid flow can be split into two non-interacting portions; a thin layer close to the surface governed by viscosity (the stickiness of the fluid) and an inviscid mainstream. This allowed Prandtl and his colleagues to make much more accurate predictions of the lift and drag performance of specific wing-shapes and greatly helped in the design of German WWI aircraft. In 1917 Prandtl showed that Junker’s thick and less-cambered aerofoil section produced much more favourable lift characteristics than the classic thinner sections used by Germany’s enemies. Second, the thick aerofoil could be flown at a much higher angle of attack without stalling and hence improved the manoeuvrability of a plane during dog fighting.
Skin Friction versus Pressure Drag
The flow in a boundary layer can be either laminar or turbulent. Laminar flow is orderly and stratified without interchange of fluid particles between individual layers, whereas in turbulent flow there is significant exchange of fluid perpendicular to the flow direction. The type of flow greatly influences the physics of the boundary layer. For example, due to the greater extent of mass interchange, a turbulent boundary layer is thicker than a laminar one and also features a steeper velocity gradient close to the surface, i.e. the flow speed increases more quickly as we move away from the wall.
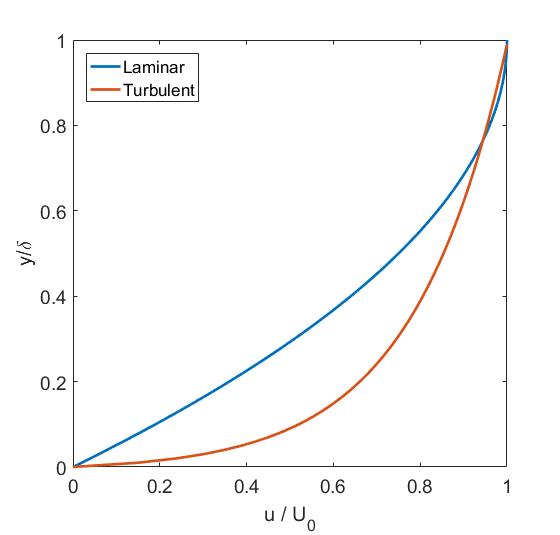
Velocity profile of laminar versus turbulent boundary layer. Note how the turbulent flow increases velocity more rapidly away from the wall.
Just like your hand experiences friction when sliding over a surface, so do layers of fluid in the boundary layer, i.e. the slower regions of the flow are holding back the faster regions. This means that the velocity gradient throughout the boundary layer gives rise to internal shear stresses that are akin to friction acting on a surface. This type of friction is aptly called skin-friction drag and is predominant in streamlined flows where the majority of the body’s surface is aligned with the flow. As the velocity gradient at the surface is greater for turbulent than laminar flow, a streamlined body experiences more drag when the boundary layer flow over its surfaces is turbulent. A typical example of a streamlined body is an aircraft wing at cruise, and hence it is no surprise that maintaining laminar flow over aircraft wings is an ongoing research topic.
Over flat surfaces we can suitably ignore any changes in pressure in the flow direction. Under these conditions, the boundary layer remains stable but grows in thickness in the flow direction. This is, of course, an idealised scenario and in real-world applications, such as curved wings, the flow is most likely experiencing an adverse pressure gradient, i.e. the pressure increases in the flow direction. Under these conditions the boundary layer can become unstable and separate from the surface. The boundary layer separation induces a second type of drag, known as pressure drag. This type of drag is predominant for non-streamlined bodies, e.g. a golfball flying through the air or an aircraft wing at a high angle of attack.
So why does the flow separate in the first place?
To answer this question consider fluid flow over a cylinder. Right at the front of the cylinder fluid particles must come to rest. This point is aptly called the stagnation point and is the point of maximum pressure (to conserve energy the pressure needs to fall as fluid velocity increases, and vice versa). Further downstream, the curvature of the cylinder causes the flow lines to curve, and in order to equilibrate the centripetal forces, the flow accelerates and the fluid pressure drops. Hence, an area of accelerating flow and falling pressure occurs between the stagnation point and the poles of the cylinder. Once the flow passes the poles, the curvature of the cylinder is less effective at directing the flow in curved streamlines due to all the open space downstream of the cylinder. Hence, the curvature in the flow reduces and the flow slows down, turning the previously favourable pressure gradient into an adverse pressure gradient of rising pressure.
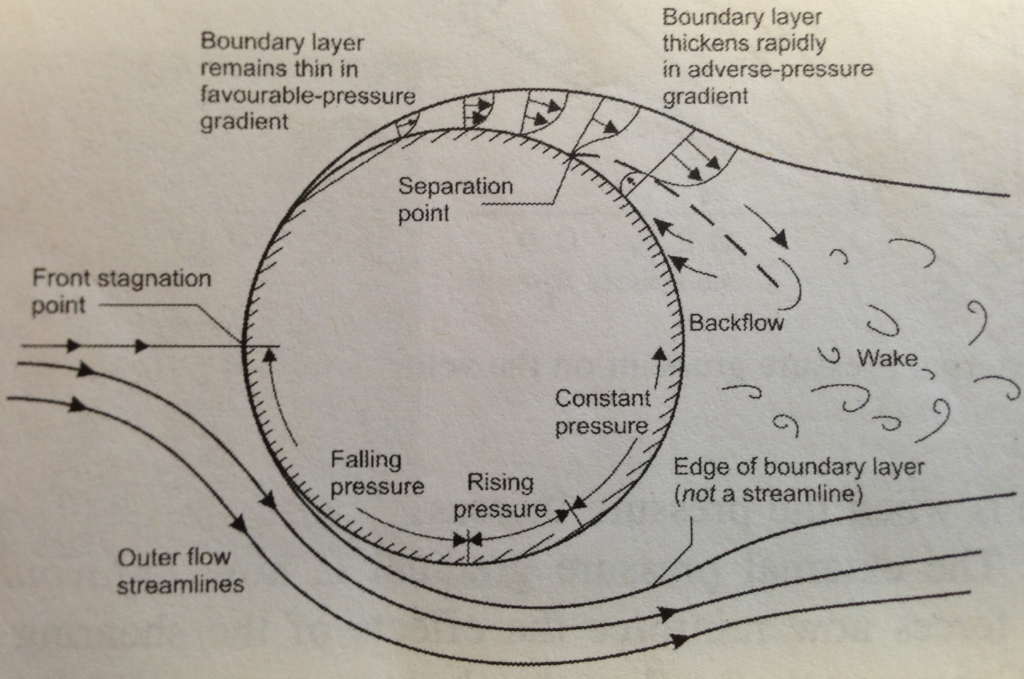
Boundary layer separation over a cylinder (axis out out the page).
To understand boundary layer separation we need to understand how these favourable and adverse pressure gradients influence the shape of the boundary layer. From our discussion on boundary layers, we know that the fluid travels slower the closer we are to the surface due to the retarding action of the no-slip condition at the wall. In a favourable pressure gradient, the falling pressure along the streamlines helps to urge the fluid along, thereby overcoming some of the decelerating effects of the fluid’s viscosity. As a result, the fluid is not decelerated as much close to the wall leading to a fuller U-shaped velocity profile, and the boundary layer grows more slowly.
By analogy, the opposite occurs for an adverse pressure gradient, i.e. the mainstream pressure increases in the flow direction retarding the flow in the boundary layer. So in the case of an adverse pressure gradient the pressure forces reinforce the retarding viscous friction forces close to the surface. As a result, the difference between the flow velocity close to the wall and the mainstream is more pronounced and the boundary layer grows more quickly. If the adverse pressure gradient acts over a sufficiently extended distance, the deceleration in the flow will be sufficient to reverse the direction of flow in the boundary layer. Hence the boundary layer develops a point of inflection, known as the point of boundary layer separation, beyond which a circular flow pattern is established.
For aircraft wings, boundary layer separation can lead to very significant consequences ranging from an increase in pressure drag to a dramatic loss of lift, known as aerodynamic stall. The shape of an aircraft wing is essentially an elongated and perhaps asymmetric version of the cylinder shown above. Hence the airflow over the top convex surface of a wing follows the same basic principles outlined above:
- There is a point of stagnation at the leading edge.
- A region of accelerating mainstream flow (favourable pressure gradient) up to the point of maximum thickness.
- A region of decelerating mainstream flow (adverse pressure gradient) beyond the point of maximum thickness.
These three points are summarised in the schematic diagram below.
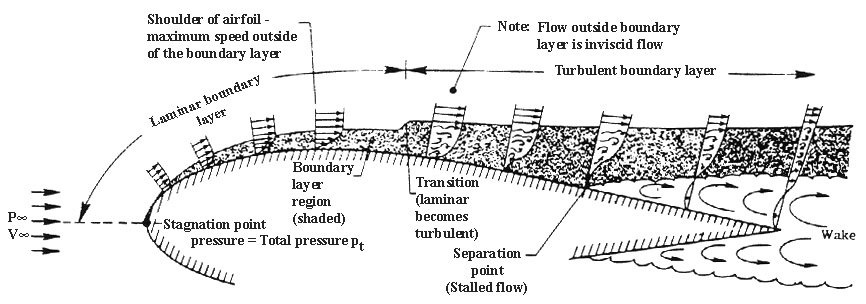
Boundary layer separation over the top surface of a wing.
Boundary layer separation is an important issue for aircraft wings as it induces a large wake that completely changes the flow downstream of the point of separation. Skin-friction drag arises due to inherent viscosity of the fluid, i.e. the fluid sticks to the surface of the wing and the associated frictional shear stress exerts a drag force. When a boundary layer separates, a drag force is induced as a result of differences in pressure upstream and downstream of the wing. The overall dimensions of the wake, and therefore the magnitude of pressure drag, depends on the point of separation along the wing. The velocity profiles of turbulent and laminar boundary layers (see image above) show that the velocity of the fluid increases much slower away from the wall for a laminar boundary layer. As a result, the flow in a laminar boundary layer will reverse direction much earlier in the presence of an adverse pressure gradient than the flow in a turbulent boundary layer.
To summarise, we now know that the inherent viscosity of a fluid leads to the presence of a boundary layer that has two possible sources of drag. Skin-friction drag due to the frictional shear stress between the fluid and the surface, and pressure drag due to flow separation and the existence of a downstream wake. As the total drag is the sum of these two effects, the aerodynamicist is faced with a non-trivial compromise:
- skin-friction drag is reduced by laminar flow due to a lower shear stress at the wall, but this increases pressure drag when boundary layer separation occurs.
- pressure drag is reduced by turbulent flow by delaying boundary layer separation, but this increases the skin-friction drag due to higher shear stresses at the wall.
As a result, neither laminar nor turbulent flow can be said to be preferable in general and judgement has to be made regarding the specific application. For a blunt body, such as a cylinder, pressure drag dominates and therefore a turbulent boundary layer is preferable. For more streamlined bodies, such as an aircraft wing at cruise, the overall drag is dominated by skin-friction drag and hence a laminar boundary layer is preferable. Dolphins, for example, have very streamlined bodies to maintain laminar flow. Early golfers, on the other hand, realised that worn rubber golf balls flew further than pristine ones, and this led to the innovation of dimples on golf balls. Fluid flow over golf balls is predominantly laminar due to the relatively low flight speeds. Dimples are therefore nothing more than small imperfections that transform the predominantly laminar flow into a turbulent one that delays the onset of boundary layer separation and therefore reduces pressure drag.
Aerodynamic Stall
The second, and more dramatic effect, of boundary layer separation in aircraft wings is aerodynamic stall. At relatively low angles of attack, for example during cruise, the adverse pressure gradient acting on the top surface of the wing is benign and the boundary layer remains attached over the entire surface. As the angle of attack is increased, however, so does the pressure gradient. At some point the boundary layer will start to separate near the trailing edge of the wing, and this separation point will move further upstream as the angle of attack is increased. If an aerofoil is positioned at a sufficiently large angle of attack, separation will occur very close to the point of maximum thickness of the aerofoil and a large wake will develop behind the point of separation. This wake redistributes the flow over the rest of the aerofoil and thereby significantly impairs the lift generated by the wing. As a result, the lift produced is seriously reduced in a condition known as aerodynamic stall. Due to the high pressure drag induced by the wake, the aircraft can further lose airspeed, pushing the separation point further upstream and creating a deleterious feedback loop where the aircraft literally starts to fall out of the sky in an uncontrolled spiral. To prevent total loss of control, the pilot needs to reattach the boundary as quickly as possible which is achieved by reducing the angle of attack and pointing the nose of the aircraft down to gain speed.
The lift produced by a wing is given by
where 
During cruise the angle of attack is relatively small (
High-lift Devices
A much more elegant solution are leading-edge slats and trailing-edge flaps. A slat is a thin, curved aerofoil that is fitted to the front of the wing and is intended to induce a secondary airflow through the gap between the slat and the leading edge. The air accelerates through this gap and thereby injects high momentum fluid into the boundary on the upper surface, delaying the onset of flow reversal in the boundary layer. Similarly, one or two curved aerofoils may be placed at the rear of wing in order to invigorate the flow near the trailing edge. In this case the high momentum fluid reinvigorates the flow which has been slowed down by the adverse pressure gradient. The maximum lift coefficient can typically be doubled by these devices and therefore allows big jumbo jets to land and takeoff at relatively low runway speeds.
Leading edge slats and trailing edge flaps on an aircraft wing
The next time you are sitting close to the wings observe how these devices are retracted after take-off and activated before landing. In fact, birds have a similar devices on their wings. The wings of bats are comprised of thin and flexible membranes reinforced by small bones which roughen the membrane surface and help to transition the flow from laminar to turbulent and prevent boundary layer separation. As is so often the case in engineering design, a lot of inspiration can be taken from nature!
In the first paragraph of section “modern plane – born in 1915 “, you might confuse people with the phrase “aerodynamic centre (the point where the lift force can be considered to act)”. Aerodynamic centre is the point about which moment doesn’t change but not necessarily zero. It is the centre of pressure at which lift is considered to act because net moment about it is zero. But we often put the lift at aerodynamic centre ( and add moment to account for difference in positions of aerodynamic and pressure centers) because it is easier to do math when moment doesn’t change with angle of attack.
Centre of pressure is not used usually because it’s position changes with angle of attack whereas aerodynamic centre, by definition, doesn’t.
Raghu,
thanks for your comment. You’re right, that was entirely my mistake. Aerodynamic centre should be centre of pressure. Don’t know why I swapped the two around. Thanks for pointing it out!
Rainer
When the lift coefficient is maximum for an airfoil, does it mean that the separation point is on the leading edge? Can separation from a point down the chord cause maximum lift (and stall after that) defined by the Cl vs AOA curve)?
Hi, no maximum lift does not necessarily correspond to the separation point being at the leading edge. As the AoA is increased the lift coefficient increases too; initially, in a linear relationship. But the increase in AoA also leads to some separation close to the trailing edge, which moves closer to the leading edge as the AoA increases. Therefore, the closer we get to stall the more the relationship between lift coefficient and AoA becomes non-linear. An incremental change of AoA does not lead to the same degree of incremental lift coefficient anymore (slope of the Cl – AoA curve decreases). This means the maximum lift coefficient typically occurs before separation reaches the leading edge. This video has some nice visualisations: https://www.youtube.com/watch?v=q_eMQvDoDWk
Thank you for your explanation!!
May I ask the source of the picture “Boundary layer separation over a cylinder (axis out out the page).”
It’s from one of my lecture notes when I was an undergraduate student. But you can find many other versions online. For example here: https://people.rit.edu/pnveme/personal/MECE356/drag/flowcyl_model.jpg
and also: C. B. Millikan – Aerodynamics of an Airplane
Rainer
No, immediately AFTER stagnation JUST before the leading edge of the airfoil do maximum pressure coefficients become salient; the threshold is then attained.
Little is said here about the flow UNDER the wing – yet this seems to be just as important in generating lift, if not more so, and I assume must have it’s own Prandtl layer. For a wing tilted upward against the airflow, the convergence of air flowing into the region must result in an increase in pressure, as well as velocity shears, and the subsequent turbulent layer thereby generated will slow the flow and therefore increase the air density and subsequent pressure. As a result air flowing under the wing moves more slowly than that above, and such air reaches the tail of the wing quite a bit LATER than that flowing over the top (in violation of the old, simple, and incorrect, “Bernoulli explanation” of flight). Control of the underside Prandtl layer (assuming it exists) is, I suspect, critical to a least the flight of gliding birds e.g. owls, and I suspect is also critical to understanding flight in general. Such a model also explains why aircraft can fly upside-down, if the angle of attack is correct. Am I incorrect?
Hi Wayne, thanks for your comment. You are absolutely right, the bottom surface of an airfoil plays an important role in creating lift. The topic of this article was not particularly about the creation of lift per se, but more about the idea of pressure drag and how it is created. Of course lift and pressure drag are both aerodynamic phenomena, and thus, closely related. But the main focus here is pressure drag, and to illustrate its source, talking about the top surface is sufficient. There is indeed another article on this webpage dealing just with lift (https://aerospaceengineeringblog.com/how-do-wings-work/) and a discussion at the bottom with an aerodynamicist.
Thanks – I looked at the link – it is quite good. These 2 articles will be good for my first year engineering students. The one thing that I think could be added to really emphasize the importance of viscosity is a reference to Kelvin’s circulation theorem. This basically says that in an inviscid fluid, no non-rotating body can generate a force, so nothing can fly. This, perhaps parodoxically, tells us the you must have viscosity in order to fly. Aircraft essentially float on a cushion of controlled turbulence (Prandtl layer). Einstein is reputed to have spent some time developing aircraft theory for flight in an inviscid fluid – pity he had not read Kelvin’s work. Bernoulli’ theorem also really only applies for inviscid fluids (compressible or incompressible) so it really does not have too much relevance – I am not aware of a version of Bernoulli which includes viscosity, and I am not sure it is even possible to have one – the details of viscous and turbulent flow cannot be sufficiently simplified, I fear.
As you say, there is a lot of misunderstanding out there, and your articles do a good job of demystifying the process.
So I have a doubt. If the AoA increases boundary layer separation occurs earlier So, does the pressure of the wake increase or decrease?
It increases right?
I have this confusion . When the AoA(Angle of attack) is increased for a wing, due to the formation of boundary layer separation, so there will be formation of wakes(eddies ) , so the static pressure will increase(because the fluid will lose energy and come to rest) and this will reduce lift.(Also there is another reason due to newton’s third law, the fluid doesn’t flow down so there will be no transfer of momentum upwards.).
So my question is if static pressure in the right side of the wing increases then drag should reduce right? Because the pressure difference at the front and back will decrease?
Hi, maybe the example of flow around a cylinder will help. Imagine the flow stays entirely attached to the cylinder all around its circumference, such that no wake occurs at all. Now the pressure at the front and back of the cylinder is balanced, and in this theoretical scenario, we only have drag from skin friction. However, if the boundary layer does separate from the cylinder, then the pressure on the downstream side in the wake is essentially constant and equal to the lower pressure on the top and bottom of the cylinder, or essentially at the point where the flow separates. This pressure is lower than the large pressure at the stagnation point at the front of the cylinder. This pressure imbalance between front and back then leads to pressure drag.
Hi Rainer,
I just came across your blog, very clear and interesting. I take the chance to expose a question I have worked on for a couple of weeks now. I had the chance to fly in the flight deck, on a A321-200SL. During the take off, I noticed a vibration coming from the wings and I already made the observatio as a passenger some years ago. The vibration comes as soon as the AoA changes from prox 0 to about 10 to 15 ° to reach the initial climbing rate. Some people told me it would be due to the gear bay doors opening that would generate turbulence but vibration occurs as soon as the aircraft takes AoA positive I.e as soon as the nose wheel leaves the pavement. My intuition is the following: as the wing changes rapidly AoA, the boundary layer is in an unstable condition like it sticks to the wing skin then as the AoA changes it moves on the wing and then sticks back to the skin. Then the AoA changes in a matter of secs or less, so it moves again and sticks back…and so on till the rotate is complete and thus, creating vibration during about 10 sec. What do u think about my guess ? Thanks!
What happens to the skin friction drag and pressure drag for an airfoil if the
point of transition moves upstream? What is the effect on flow separation
when the point of transition moves upstream?
Is this correct? “The velocity profiles of turbulent and laminar boundary layers (see image above) show that the velocity of the fluid increases much slower away from the wall for a laminar boundary layer.” It doesn’t seem to match the drawing. The distance perpendicular to the surface past the transition point appears to much further, which is the turbulent boundary layer. What am I missing?