Rocket Science 101: Lightweight rocket shells

This is the fourth and final part of a series of posts on rocket science. Part I covered the history of rocketry, Part II dealt with the operating principles of rockets and Part III looked at the components that go into the propulsive system.

One of the most important drivers in rocket design is the mass ratio, i.e. the ratio of fuel mass to dry mass of the rocket. The greater the mass ratio the greater the change in velocity (delta-v) the rocket can achieve. You can think of delta-v as the pseudo-currency of rocket science. Manoeuvres into orbit, to the moon or any other point in space are measured by their respective delta-v’s and this in turn defines the required mass ratio of the rocket.

For example, at an altitude of 200 km an object needs to travel at 7.8 km/s to inject into low earth orbit (LEO). Accounting for frictional losses and gravity, the actual requirement rocket scientists need to design for when starting from rest on a launch pad  is just shy of delta-v=10 km/s. Using Tsiolovsky’s rocket equation and assuming a representative average exhaust velocity of 3500 m/s, this translates into a mass ratio of 17.4:

A mass ratio of 17.4 means that the rocket needs to be % fuel!

This simple example explains why the mass ratio is a key indicator of a rocket’s structural efficiency. The higher the mass ratio the greater the ratio of delta-v producing propellant to non-delta-v producing structural mass. The simple example also explains why staging is such an effective strategy. Once, a certain amount of fuel within the tanks has been used up, it is beneficial to shed the unnecessary structural mass that was previously used to contain the fuel but is no longer contributing to delta-v.

At the same time we need to ask ourselves how to best minimise the mass of the rocket structure?

So in this post we will turn to my favourite topic of all: Structural design. Let’s dig in…

The role of the rocket structure is to provide some form of load-bearing frame while simultaneously serving as an aerodynamic profile and container for propellant and payload. In order to maximise the mass ratio, the rocket designer wants to minimise the structural mass that is required to safely contain the propellant. There are essentially two ways to achieve this:

• Using lightweight materials.
• And/or optimising the geometric design of the structure.

When referring to “lightweight materials” what we mean is that the material has high values of specific stiffness, specific strength and/or specific toughness. In this case “specific” means that the classical engineering properties of elastic modulus (stiffness), yield or ultimate strength, and fracture toughness are weighted by the density of the material. For example, if a design of given dimensions (fixed volume) requires a certain stiffness and strength, and we can achieve these specifications with a material of superior specific properties, then the mass of the structure will be reduced compared to some other material. In the rocket industry the typical materials are aerospace-grade titanium and aluminium alloys as their specific properties are much more favourable than those of other metal alloys such as steel.

However, over the last 30 years there has been a drive towards increasing the proportion of advanced fibre-reinforced plastics in rocket structures. One of the issues with composites is that the polymer matrices that bind the fibres together become rather brittle (think of shattering glass) under the cryogenic temperatures of outer space or when in contact with liquid propellants. The second issue with traditional composites is that they are more flammable; obviously not a good thing when sitting right next to liquid hydrogen and oxygen. Third, it is harder to seal composite rocket tanks and especially bolted joints are prone to leaking. Finally, the high-performance characteristics that are needed for space applications require the use of massive high-pressure, high-temperature ovens (autoclaves) and tight-tolerance moulds which significantly drive up manufacturing costs. For these reasons the use composites is mostly restricted to payload fairings. NASA is currently working hard on their out-of-autoclave technology and automated fibre placement technology, while RocketLabs have announced that they will be designing a carbon-composite rocket too, and I would expect this technology to mature over the next decade.

The load-bearing structure in a rocket is very similar to the fuselage of an airplane and is based on the same design philosophy: semi-monocoque construction. In contrast to early aircraft that used frames of discrete members braced by wires to sustain flight loads and flexible membranes as lift surfaces, the major advantage of semi-monocoque construction is that the functions of aerodynamic profile and load-carrying structure are combined. Hence, the visible cylindrical barrel of a rocket serves to contain the internal fuel as a pressure vessel, sustains the imposed flights loads and also defines the aerodynamic shape of the rocket. Because the external skin is a working part of the structure, this type of construction is known as stressed skin or monocoque. The even distribution of material in a monocoque means that the entire structure is at a more uniform and lower stress state with fewer local stress concentrations that can be hot spots for crack initiation.

Second, curved shell structures, as in a cylindrical rocket barrel, are one of the most efficient forms of construction found in nature, e.g. eggs, sea-shells, nut-shells etc.. In thin-walled curved structures the external loads are reacted internally by a combination of membrane stresses (uniform stretching or compression through the thickness) and bending stresses (linear variation of stresses through the thickness with tension on one side, compression on the other side, zero stress somewhere in the interior of the thickness known as the neutral axis). As a rule of thumb, membrane stresses are more efficient than bending stresses, as all of the material through the thickness is contributing to reacting the external load (no neutral axis) and the stress state is uniform (no stress concentrations).

In general, flat structures such as your typical credit card, will resist tensile and compressive external loads via uniform membrane stresses, and bending via linearly varying stresses through the thickness. The efficiency of curved shells stems from the fact that membrane stresses are induced to react both uniform stretching/compressive forces and bending moments. The presence of a membrane component reduces the peak stress that occurs through the thickness of the shell, and ultimately means that a thinner wall thickness and associated lower component mass will safely resist the externally applied loads. This is important as the bending stiffness of thin-walled structures is typically at least an order of magnitude smaller than the stretching/compressive stiffness (e.g. you can easily bend your credit card, but try stretching it).

Bending and membrane stress states

Alas, as so often in life, there is a compromise. Optimising a structure for one mode of deformation typically makes it more fragile in another. This means that if the structure fails in the deformation mode that it has been optimised for, the ensuing collapse is most-likely sudden and catastrophic.

As described above, reducing the wall-thickness in a monocoque construction greatly helps to reduce the mass of the structure. However, the bending stiffness scales with the cube of the thickness, whereas the membrane stiffness only scales linearly. Hence, in a thin-walled structure we ideally want all deformation to be in a membrane state (uniform squashing or stretching), and curved shell structures help to guarantee this. However, due to the large mismatch between membrane stiffness and bending stiffness in a thin-walled structure, the structure may at some point energetically prefer to bend and will transition to a bending state.

This phenomenon is known as buckling and is the bane of thin-walled construction.

One of the principles of physics is that the deformation of a structure is governed by the proclivity to minimise the strain energy. Hence, a structure can at some point bifurcate into a different deformation shape if this represents a lower energy state. As a little experiment, form a U-shape with your hand, thumb on one side and four fingers on the other. Hold a credit card between your thumb and the four fingers and start to compress it. Initially, the structure reacts this load by compressing internally (membrane deformation) in a flat state, but very soon the credit card will snap one way to form a U-shape (bending deformation).

The reason this works is because compressing the credit card reduces the distance between two edges held by the thumb and four fingers. The credit card can satisfy these new externally imposed constraints either by compressing uniformly, i.e. squashing up, or by maintaining its original length and bending into an arc. At some critical point of compression the bending state is energetically more favourable than the squashed state and the credit card bifurcates. Note that this explanation should also convince you that this form of behaviour is not possible under tension as the bifurcation to a bending state will not return the credit card to its original length.

The advantage of curved monocoques is that their buckling loads are much greater than those flat plates. For example, you can safely stand on a soda can even though it is made out of relatively cheap aluminium. However, once the soda can does buckle all hell breaks loose and the whole thing collapses in one big heap. What is more, curved structures are very susceptible to initial imperfections which drastically reduce the load at which buckling occurs. Flick the side of a soda can to initiate a little dent and stand back on the can to feel the difference.

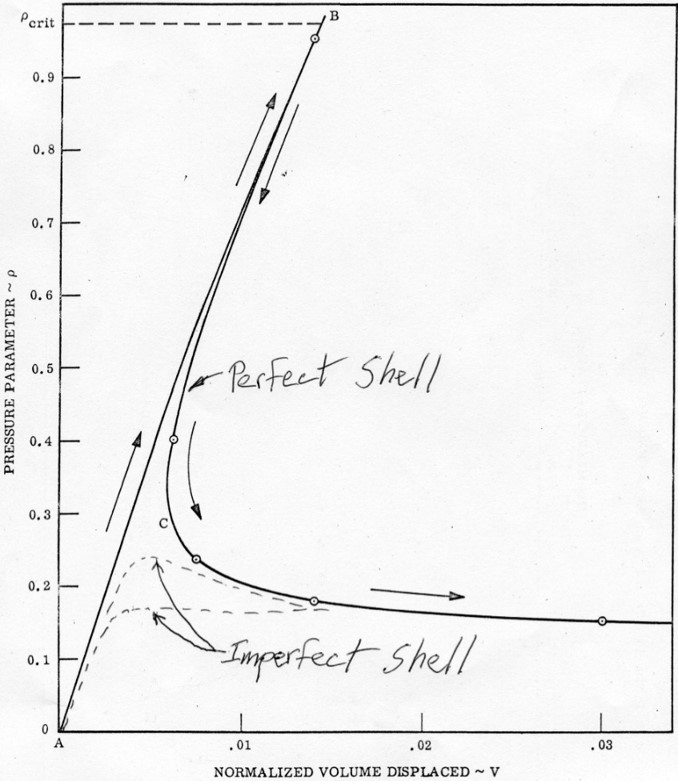
Imperfection sensitivity of a cylinder. The plot shows the drastic reduction in load (vertical axis) that the perfect cylinder can sustain with increasing deformation (horizontal axis) once the buckling point has been passed. This means that an imperfect (real) shell will never reach the maximum load but diverge to the lower load level straight away.

This problem is exacerbated by the fact that the shape of the tiny initial imperfections, typically of the order of the thickness of the shell, can lead to vastly different failure modes. Thus, the behaviour of the shell is emergent of the initial conditions. In this domain of complexity it is very difficult to make precise repeatable predictions of how the structure will behave. For this reason, curved shells are often called the “prima-donna” of structures and we need to be very careful in how we go about designing them.

A rocket is naturally exposed to compressive forces as a result of gravity and inertia while accelerating. In order to increase the critical buckling loads of the cylindrical rocket shell, the skin is stiffened by internal stiffeners. This type of construction is known as semi-monocoque to describe the discrete discontinuities of the internal stiffeners. A rocket cylinder typically has internal stringers running top to bottom and internal hoops running around the circumference of the cylindrical skin.

Space Shuttle internal structure of propellant tank. Note the circumferential hoops and longitudinal stringers that help, among other things, to increase the buckling load (via Wikimedia Commons).

The purpose of these stringers and hoops is twofold:

• First, they help to resist compressive loading and therefore remove some of the onus on the thin skin.
• Second, they break the thin skin into smaller sections which are much harder to buckle. To convince yourself, find an old out-of-date credit card, cut it in half and repeat the previously described experiment.

The cylindrical rocket shell has a second advantage in that it acts as a pressure vessel to contain the pressurised propellants. The internal pressure of the propellants increases the circumference of the rocket shell, and like blowing up a balloon, imparts tensile stretching deformations into the skin which preempt the compressive gravitational and inertial loads. In fact, this pressure-stabilisation effect is so helpful that some old rockets that you see on display in museums, most notoriously the Atlas 2E rocket, need to be pressurised artificially by external air pumps at all times to prevent them from collapsing under their own weight. If you look at the diagram below you can see little diamond-shaped dimples spread all over the skin. These are buckling waveforms.

Atlas 2E Ballistic Missile with buckling “diamonds” along the entire length of the external rocket skin (via Wikimedia Commons)

NASA Langley Research Center has been, and continues to be, a leader in studying the complex failure behaviour of rocket shells. To find out more, check out the video by some of the researchers that I have worked with who are developing new methods of designing the next generation of composite rocket shells.