Breguet Range Equation

There is a saying that your audience will halve for every equation you put in a piece of writing. Well, in this case I am going to make an exception and go through the detailed derivation of the Breguet Range equation. The reason for doing this is that the maths is not very difficult but the implications of the equation are known to every pilot on earth and everyone interested in flight should know about it. Simply put, the Breguet range equation tells engineers how far and airplane can fly given a certain set of parameters, and therefore greatly influences the design of modern jet engines and airframes.

A central aspect of flying further for the same amount of fuel is maximising the lift to drag ratio of your wings and airframe. Optimising this ratio gives the maximum aircraft weight (=lift at steady horizontal flight) that can be kept in the air for a given amount of engine thrust (=drag at steady horizontal flight). However, this parameter is not the primary optimum for commercial flight. Instead one wants to fly the furthest possible distance with one fuel filling. Thus to achieve the maximum possible range the quantity to be optimised is the product of flight speed (U) with lift (L) to drag (D) ratio . For most long-haul journeys (~12 hours) the most time consuming part of the journey, and therefore most critical for fuel consumption is the cruise condition. During cruise conditions the band of altitudes that the airliner travels through does not vary greatly such that the local speed of sound   where T is the local static temperature, does not vary greatly. Consequently optimising the Mach Number  times the lift to drag ratio  is virtually the same.

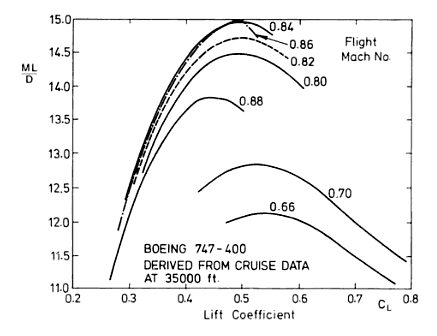
Figure 1 shows experimental data of this parameter versus the lift-coefficient   for a Boeing 747-400 at 35,000 ft. At each Mach number L/D rises to a maximum until further increase in lift coefficient leads to stall of the aerofoil. At lower flight speeds the boundary layer separation will occur naturally towards the trailing edge but as we approach a flight speed of Mach 1 shock waves also come into play. The graph shows that for all cruise speeds the optimum value of   occurs at a lift coefficient of about 0.5. The wing area S of an aeroplane is set largely by conditions at take-off and landing, such that it is hard to continually operate at a lift coefficient of 0.5 as the weight and therefore lift of the aeroplane decreases as fuel is burnt. To operate as close to optimum on can therefore decrease v, not very attractive, or decrease the density by flying at higher altitudes. Large airliners therefore typically start cruise at 31 000 ft or higher and then increase altitude in steps to fly at the optimum .

Fig. 1. Mach number x lift-drag versus lift coefficient for various flight Mach numbers (1).

The global maximum is achieved for a cruise speed of M = 0.86. Beyond this point   can be seen to fall precipitously. Since the air accelerates over the top surface of the aerofoil flight speeds close to Mach 1 can lead to local pockets of supersonic flow over the airflow. At some point these supersonic pockets terminate in a lambda shock wave across which the local air pressure increases to obey the law of thermodynamics. This increase in pressure exacerbates the adverse pressure gradient along the length of the aerofoil, leading to earlier boundary layer separation and an induced increase in drag. Furthermore, the separation caused by shock waves leads to buffeting and control problems. For this reason the typical Mach Number during cruise is set around 0.85.

The next time you fly you could easily check this using one of the onboard screens that display flight data. Take the formula , and set U equal to flight speed in meters/second (= km/hr divided by 3.6), ratio of specific heat capacity , gas constant and local temperature T in Kelvin = T in °C +273. Alternatively replacing all values in the equation we get . Typical flight conditions are 880 km/hr at -60°C giving a Mach Number of 0.83.

The conventional measure of the amount of fuel used compared to the thrust produced is the specific fuel conusmption (SFC). The SFC is the fuel mass-flow rate divided by the thrust produced and therefore has units of kg/(Ns). At cruise, the rate of change of weight (dW/dt) is proportional to the fuel mass-flow rate , , such that,

The negative sign indicates that the weight of the aeroplane is decreasing with time as fuel is burnt. The SFC is,

and since F = D for horizontal cruise we have,

Since W=L for horizontal cruise,

For constant speed U the distance travelled is dx = U*dt, hence

If SFC, U and L/D are constant this expression can be integrated to give the final result,

where are the initial and final weights during cruise. This equation is known as the Breguet Range equation. We discussed before that  should be optimised to increase range. However, it can be noted that the range is inversely proportional to the SFC and since SFC is also a function of the flight speed U the situation is a bit more complicated. In reality the aim is to maximise the ratio of . Of course SFC also depends on the efficiency of the jet engines, which has been discussed in a series of previous posts (1,2,3). Furthermore, the structural weight is crucial forming a large part of . Finally the aerodynamic profile of the whole aircraft has to be optimised in order to reduce drag and thereby decrease the thrust F required to overcome it.

References

(1) Cumpsty, N.A. (2003). Jet Propulsion: A Simple Guide to the Aerodynamic and Thermodynamic Design and Performance of Jet Engines. Cambridge University Press.